Atmospheric pressure

"Air pressure" redirects here. For the pressure of air in other systems, see Pressure.

Atmospheric pressure, also known as air pressure or barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as 101,325 Pa (1,013.25 hPa), which is equivalent to 1,013.25 millibars, 760 mm Hg, 29.9212 inches Hg, or 14.696 psi. The atm unit is roughly equivalent to the mean sea-level atmospheric pressure on Earth; that is, the Earth's atmospheric pressure at sea level is approximately 1 atm.

In most circumstances, atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point. As elevation increases, there is less overlying atmospheric mass, so atmospheric pressure decreases with increasing elevation. Because the atmosphere is thin relative to the Earth's radius—especially the dense atmospheric layer at low altitudes—the Earth's gravitational acceleration as a function of altitude can be approximated as constant and contributes little to this fall-off. Pressure measures force per unit area, with SI units of pascals (1 pascal = 1 newton per square metre, 1 N/m²). On average, a column of air with a cross-sectional area of 1 square centimetre (cm²), measured from the mean (average) sea level to the top of Earth's atmosphere, has a mass of about 1.03 kilogram and exerts a force or "weight" of about 10.1 newtons, resulting in a pressure of 10.1 N/cm² or 101 kN/m² (101 kilopascals, kPa). A column of air with a cross-sectional area of 1 in² would have a weight of about 14.7 lbf, resulting in a pressure of 14.7 lbf/in².

Mechanism

Atmospheric pressure is caused by the gravitational attraction of the planet on the atmospheric gases above the surface and is a function of the mass of the planet, the radius of the surface, and the amount and composition of the gases and their vertical distribution in the atmosphere. It is modified by the planetary rotation and local effects such as wind velocity, density variations due to temperature and variations in composition.

Mean sea-level pressure

Map showing atmospheric pressure in mbar or hPa

15-year average mean sea-level pressure for June, July, and August (top) and December, January, and February (bottom). ERA-15 re-analysis.

Kollsman-type barometric aircraft altimeter.

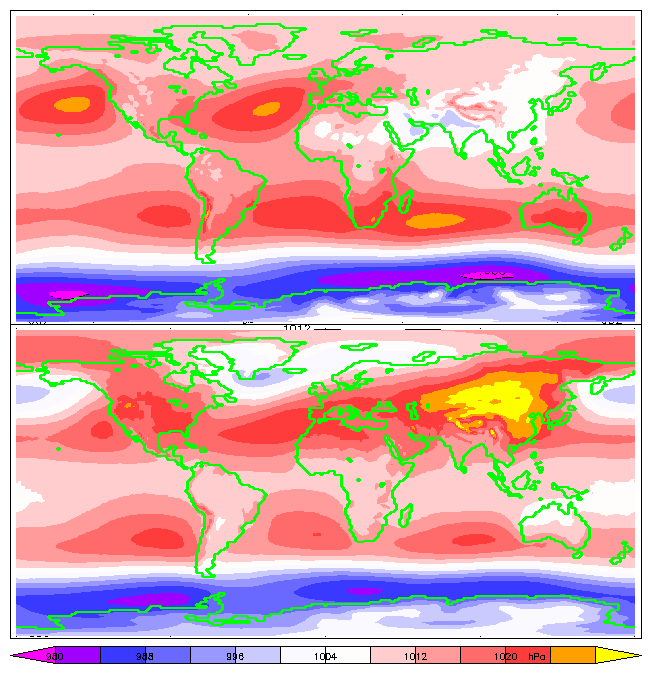
The mean sea-level pressure (MSLP) is the atmospheric pressure at mean sea level. This is the atmospheric pressure normally given in weather reports on radio, television, and newspapers or on the Internet.

The altimeter setting in aviation is an atmospheric pressure adjustment.

Average sea-level pressure is 1,013.25 hPa (29.921 inHg; 760.00 mmHg). In aviation weather reports (METAR), QNH is transmitted around the world in hectopascals or millibars (1 hectopascal = 1 millibar). In the United States, Canada, and Japan altimeter setting is reported in inches of mercury (to two decimal places). The United States and Canada also report sea-level pressure SLP, which is adjusted to sea level by a different method, in the remarks section, not in the internationally transmitted part of the code, in hectopascals or millibars. However, in Canada's public weather reports, sea level pressure is instead reported in kilopascals.

In the US weather code remarks, three digits are all that are transmitted; decimal points and the one or two most significant digits are omitted: 1,013.2 hPa (14.695 psi) is transmitted as 132; 1,000 hPa (100 kPa) is transmitted as 000; 998.7 hPa is transmitted as 987; etc. The highest sea-level pressure on Earth occurs in Siberia, where the Siberian High often attains a sea-level pressure above 1,050 hPa (15.2 psi; 31 inHg), with record highs close to 1,085 hPa (15.74 psi; 32.0 inHg). The lowest measurable sea-level pressure is found at the centres of tropical cyclones and tornadoes, with a record low of 870 hPa (12.6 psi; 26 inHg). A system transmitting the last three digits transmits the same code (800) for 1080.0 hPa as for 980.0 hPa.

Surface pressure

This section is about the atmospheric surface pressure. For other uses, see Surface pressure (disambiguation).

Surface pressure is the atmospheric pressure at a location on Earth's surface (terrain and oceans). It is directly proportional to the mass of air over that location.

For numerical reasons, atmospheric models such as general circulation models (GCMs) usually predict the nondimensional logarithm of surface pressure.

The average value of surface pressure on Earth is 985 hPa. This is in contrast to mean sea-level pressure, which involves the extrapolation of pressure to sea level for locations above or below sea level. The average pressure at mean sea level (MSL) in the International Standard Atmosphere (ISA) is 1,013.25 hPa, or 1 atmosphere (atm), or 29.92 inches of mercury.

Pressure (P), mass (m), and acceleration due to gravity (g) are related by P = F/A = (m*g)/A, where A is the surface area. Atmospheric pressure is thus proportional to the weight per unit area of the atmospheric mass above that location.

Altitude variation

Further information: Barometric formula and Vertical pressure variation

Cloud formation above Snæfellsjökull (Iceland), formed above the mountain by orographic lift

Variation in atmospheric pressure with altitude, computed for 15 °C and 0% relative humidity.

This plastic bottle was sealed at approximately 4,300 metres (14,000 ft) altitude, and was crushed by the increase in atmospheric pressure, recorded at 2,700 metres (9,000 ft) and 300 metres (1,000 ft), as it was brought down towards sea level.

Pressure on Earth varies with the altitude of the surface, so air pressure on mountains is usually lower than air pressure at sea level. Pressure varies smoothly from the Earth's surface to the top of the mesosphere. Although the pressure changes with the weather, NASA has averaged the conditions for all parts of the earth year-round. As altitude increases, atmospheric pressure decreases. One can calculate the atmospheric pressure at a given altitude. Temperature and humidity also affect the atmospheric pressure. Pressure is proportional to temperature and inversely related to humidity, and both of these are necessary to compute an accurate figure. The graph Template:If mobile was developed for a temperature of 15 °C and a relative humidity of 0%.

At low altitudes above sea level, the pressure decreases by about 1.2 kPa (12 hPa) for every 100 metres. For higher altitudes within the troposphere, the following equation (the barometric formula) relates atmospheric pressure p to altitude h:

<math>\begin{align}

 p &=       p_0 \cdot \left(1 - \frac{L \cdot h}{T_0} \right)^\frac{g \cdot M}{R_0 \cdot L} \\
   &= p_0 \cdot \left(1 - \frac{g \cdot h}{c_\text{p} \cdot T_0} \right)^{\frac{c_\text{p} \cdot M}{R_0}}
      \approx p_0 \cdot \exp \left(-\frac{g \cdot h \cdot M}{T_0 \cdot R_0} \right)

\end{align}</math>

The values in these equations are:

Parameter	Description	Value
h	Height above mean sea level	m
p0	Sea level standard atmospheric pressure	101,325 Pa
L	Temperature lapse rate, = g/cp for dry air	~ 0.00976 K/m
cp	Constant-pressure specific heat	1,004.68506 J/(kg·K)
T0	Sea level standard temperature	288.15 K
g	Earth-surface gravitational acceleration	9.80665 m/s2
M	Molar mass of dry air	0.02896968 kg/mol
R0	Universal gas constant	8.314462618 J/(mol·K)

Local variation

Hurricane Wilma on 19 October 2005. The pressure in the eye of the storm was 882 hPa (12.79 psi) at the time the image was taken.

Atmospheric pressure varies widely on Earth, and these changes are important in studying weather and climate. Atmospheric pressure shows a diurnal or semidiurnal (twice-daily) cycle caused by global atmospheric tides. This effect is strongest in tropical zones, with an amplitude of a few hectopascals, and almost zero in polar areas. These variations have two superimposed cycles, a circadian (24 h) cycle, and a semi-circadian (12 h) cycle.

Records

The highest adjusted-to-sea level barometric pressure ever recorded on Earth (above 750 meters) was 1,084.8 hPa (32.03 inHg) measured in Tosontsengel, Mongolia on 19 December 2001. The highest adjusted-to-sea level barometric pressure ever recorded (below 750 meters) was at Agata in Evenk Autonomous Okrug, Russia (66°53' N, 93°28' E, elevation: 261 m, 856 ft) on 31 December 1968 of 1,083.8 hPa (32.005 inHg). The discrimination is due to the problematic assumptions (assuming a standard lapse rate) associated with reduction of sea level from high elevations.

The Dead Sea, the lowest place on Earth at 430 metres (1,410 ft) below sea level, has a correspondingly high typical atmospheric pressure of 1,065 hPa. A below-sea-level surface pressure record of 1,081.8 hPa (31.95 inHg) was set on 21 February 1961.

The lowest non-tornadic atmospheric pressure ever measured was 870 hPa (0.858 atm; 25.69 inHg), set on 12 October 1979, during Typhoon Tip in the western Pacific Ocean. The measurement was based on an instrumental observation made from a reconnaissance aircraft.

Measurement based on the depth of water

One atmosphere (101.325 kPa or 14.7 psi) is also the pressure caused by the weight of a column of freshwater of approximately 10.3 m (33.8 ft). Thus, a diver 10.3 m under water experiences a pressure of about 2 atmospheres (1 atm of air plus 1 atm of water). Conversely, 10.3 m is the maximum height to which water can be raised using suction under standard atmospheric conditions.

Low pressures, such as natural gas lines, are sometimes specified in inches of water, typically written as w.c. (water column) gauge or w.g. (inches water) gauge. A typical gas-using residential appliance in the US is rated for a maximum of 1⁄2 psi (3.4 kPa; 34 mbar), which is approximately 14 w.g. Similar metric units with a wide variety of names and notation based on millimetres, centimetres or metres are now less commonly used.

Boiling point of liquids

Boiling water

Pure water boils at 100 °C (212 °F) at earth's standard atmospheric pressure. The boiling point is the temperature at which the vapour pressure is equal to the atmospheric pressure around the liquid. Because of this, the boiling point of liquids is lower at lower pressure and higher at higher pressure. Cooking at high elevations, therefore, requires adjustments to recipes or pressure cooking. A rough approximation of elevation can be obtained by measuring the temperature at which water boils; in the mid-19th century, this method was used by explorers. Conversely, if one wishes to evaporate a liquid at a lower temperature, for example in distillation, the atmospheric pressure may be lowered by using a vacuum pump, as in a rotary evaporator.

Measurement and maps

An important application of the knowledge that atmospheric pressure varies directly with altitude was in determining the height of hills and mountains, thanks to reliable pressure measurement devices. In 1774, Maskelyne was confirming Newton's theory of gravitation at and on Schiehallion mountain in Scotland, and he needed to measure elevations on the mountain's sides accurately. William Roy, using barometric pressure, was able to confirm Maskelyne's height determinations; the agreement was within one meter (3.28 feet). This method became and continues to be useful for survey work and map making.

See also

• Atmospheric density
• Atmosphere of Earth
• Barometric formula
• Barotrauma – physical damage to body tissues caused by a difference in pressure between an air space inside or beside the body and the surrounding gas or liquid.
• Cabin pressurization – Process to maintain internal air pressure in aircraft or spacecraft
• Cavitation
• Collapsing can – an aluminium can is crushed by the atmospheric pressure surrounding it
• Effects of high altitude on humans
• High-pressure area
• International Standard Atmosphere, a tabulation of typical variations of principal thermodynamic variables of the atmosphere (pressure, density, temperature, etc.) with altitude, at middle latitudes.
• Low-pressure area
• Meteorology – Interdisciplinary scientific study of the atmosphere focusing on weather forecasting
• NRLMSISE-00, an empirical, global reference atmospheric model of the Earth from ground to space
• Plenum chamber
• Pressure
• Pressure measurement
• Standard atmosphere (unit)
• Horse latitudes

External links

• Current map of global mean sea-level pressure
• 1976 Standard Atmosphere from NASA
• Source code and equations for the 1976 Standard Atmosphere
• A mathematical model of the 1976 U.S. Standard Atmosphere
• Calculator using multiple units and properties for the 1976 Standard Atmosphere
• Calculator giving standard air pressure at a specified altitude, or altitude at which a pressure would be standard
• Calculate pressure from altitude and vice versa

Experiments

• Movies on atmospheric pressure experiments from Georgia State University's HyperPhysics website – requires QuickTime
• Test showing a can being crushed after boiling water inside it, then moving it into a tub of ice-cold water.